幾何公差の図示方法

幾何公差とは

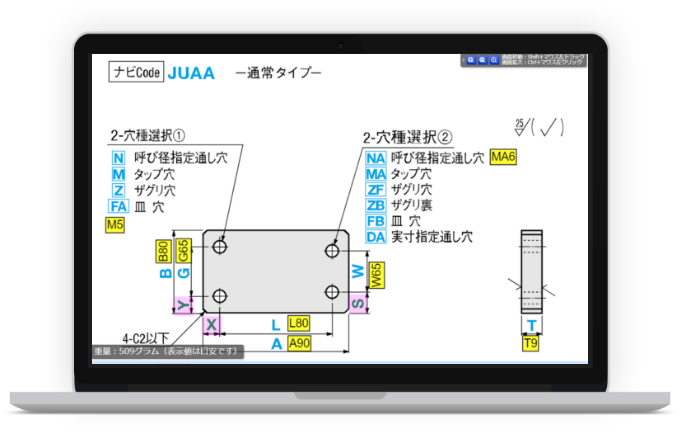
軸を穴に通す目的は、主に以下の2つがあります。１つは軸が抜けないように、穴にがっちりと固定する事。2つ目は軸が摺動できるように、穴と軸に隙間を確保する事です。
これらを区別するのが“はめあい公差“です。このはめあい公差を図面で適切に指示することで、それぞれの目的に合った軸と穴が出来上がります。

幾何公差の種類とその記号

公差の種類
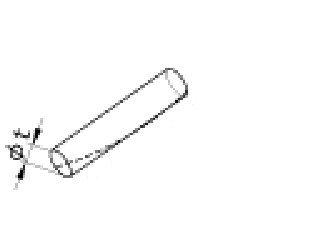
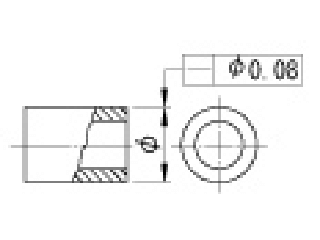
形状公差	真直度公差	公差域を示す数値の前に、記号φが付いている場合には、この公差域は直径ｔの円筒の中の領域である。	円筒の直径を示す寸法に公差記入枠が結ばれている場合には、その円筒の軸線は、直径0.08mmの円筒内になければならない。
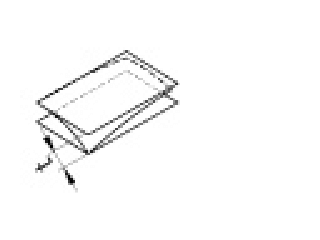
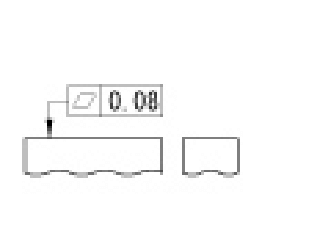
	平面度公差	公差域は、ｔだけ離れた二つの平行な平面の間に挟まれた領域である。	この表面は、0.08mmだけ離れた二つの平行な平面の間になければならない。
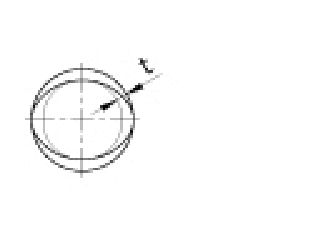
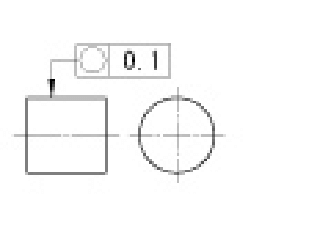
	真円度公差	対象としている平面内での公差域は、ｔだけ離れた二つの同心円の間の領域である。	任意の軸直角断面における外周は、同一平面上で0.1mmだけ離れた二つの同心円の間になければならない。
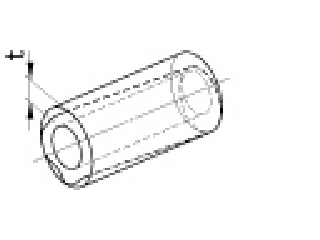
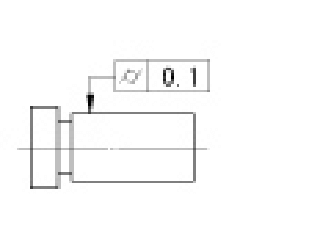
	円筒度公差	公差域は、ｔだけ離れた二つの同軸円筒面の間の領域である。	対象としている面は、0.1mmだけ離れた二つの同軸円筒面の間になければならない。
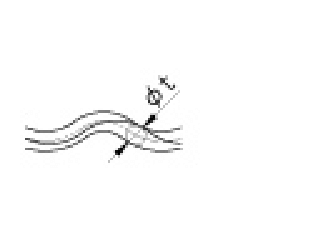
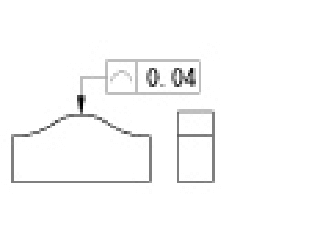
	線の輪郭度公差	公差域は、理論的に正しい輪郭線上に中心をおく、直径ｔの円がつくる二つの包絡線の間に挟まれた領域である。	投影面に平行な任意の断面で、対象としている輪郭は、理論的に正しい輪郭をもつ線の上に中心をおく直径0.04mmの円がつくる二つの包絡線の間になければならない。
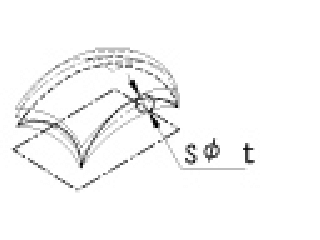
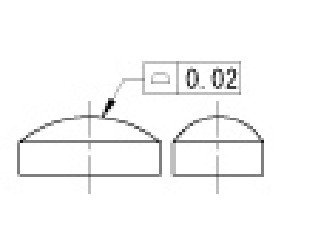
	面の輪郭度公差	公差域は、理論的に正しい輪郭面上に中心をおく、直径ｔの球がつくる二つの包絡面の間に挟まれた領域である。	対象としている面は、理論的に正しい輪郭をもつ面の上に中心をおく、直径0.02mmの球がつくる二つの包絡面の間になければならない。
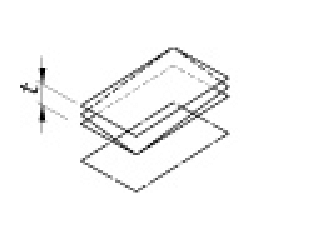
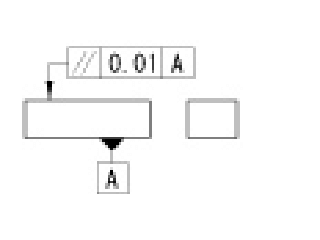
姿勢公差	平行度公差	公差域は、データム平面に平行で、ｔだけ離れた二つの平行な平面の間に挟まれた領域である。	指示線の矢で示す面は、データム平面Ａに平行で、かつ、指示線の矢の方向に0.01mmだけ離れた二つの平面の間になければならない。
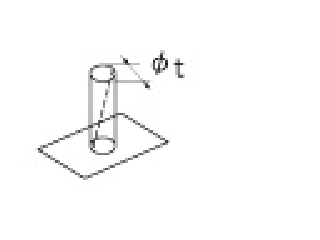
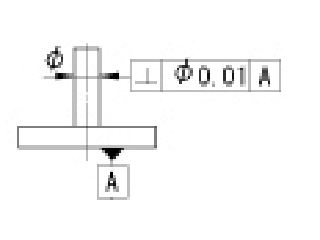
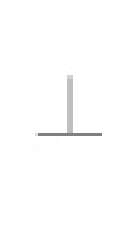
	直角度公差	公差を示す数値の前に記号φが付いている場合には、この公差域は、データム平面に垂直な直径ｔの円筒の中の領域である。	指示線の矢で示す円筒の軸線は、データム平面Ａに垂直な直径0.01mmの円筒内になければならない。
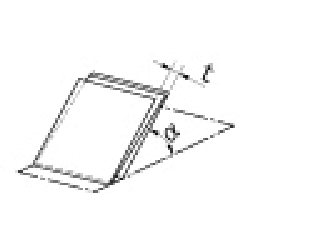
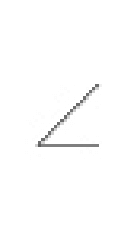
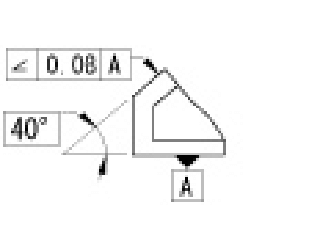
	傾斜度公差	公差域は、データム平面に対して指定された角度に傾き、互いにｔだけ離れた二つの平行な平面の間に挟まれた領域である。	指示線の矢で示す面は、データム平面Aに対して理論的に正確に40°傾斜し、指示線の矢の方向に0.08mmだけ離れた二つの平行な平面の間になければならない。
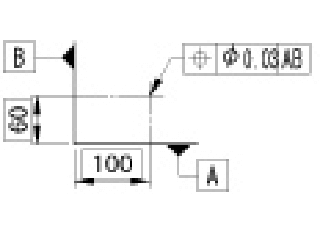
位置公差	位置度公差	公差域は、対象としている点の理論的に正確な位置（以下、真位置という）を中心とする直径ｔの円の中又は球の中の領域である。	指示線の矢で示した点は、データム直線Ａから60mm、データム直線Ｂから100mm離れた真位置を中心とする直径0.03mmの円の中になければならない。
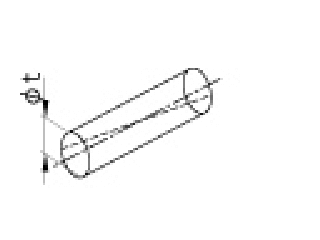
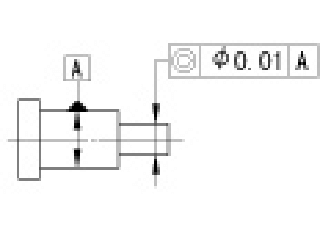
	同軸度公差又は同心度公差	公差を示す数値の前に記号φが付いている場合には、この公差域は、データム軸直線と一致した軸線をもつ直径ｔの円筒の中の領域である。	指示線の矢で示した軸線は、データム軸直線Ａを軸線とする直径0.01mmの円筒の中になければならない。
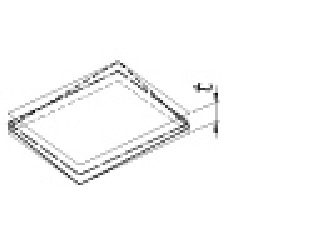
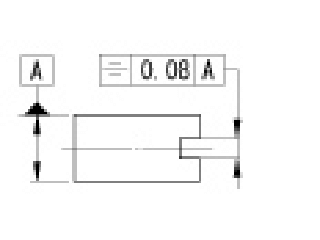
	対称度	公差域はデータム中心平面に対して対称に配置され、互いにｔだけ離れた二つの平行な平面の間に挟まれた領域である。	指示線の矢で示した中心面は、データム中心平面Ａに対称に0.08mmの間隔をもつ、平行な二つの平面の間になければならない。
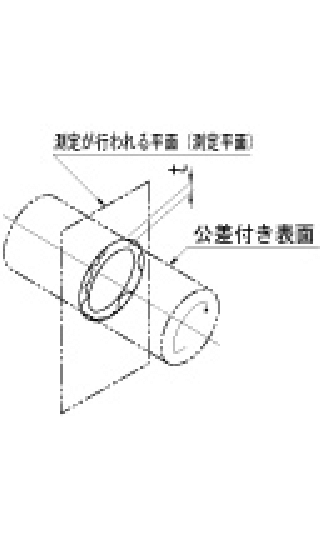
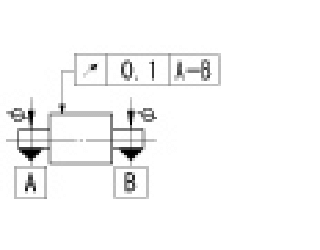
振れ公差	円周振れ公差	公差域は、データム軸直線に垂直な任意の測定平面上でデータム軸直線と一致する中心をもち、半径方向にｔだけ離れた二つの同心円の間の領域である。	指示線の矢で示す円筒面の半径方向の振れは、データム軸直線Ａ－Ｂに関して一回転させたときに、データム軸直線に垂直な任意の測定平面上で、0.1mmを超えてはならない。
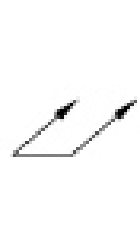
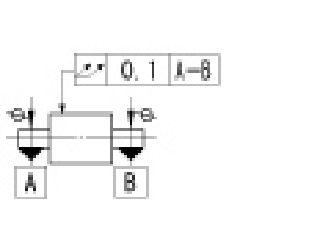
振れ公差	全振れ公差	公差域は、データム軸直線に一致する軸線をもち、半径方向にｔだけ離れた二つの同軸円筒の間の領域である。	指示線の矢で示す円筒面の半径方向の全振れは、データム軸直線Ａ－Ｂに関して円筒部分を回転させたときに、円筒表面上の任意の点で0.1mmを超えてはならない。